Общая задача линейного программирования
Дана система m линейных уравнений и неравенств с n переменными (система ограничений)
и линейная (целевая) функция
|
F = c1x1 + c2x2 + … + cnxn. |
2) |
Необходимо найти такое решение системы X = (x1, x2, …, xj, …, xn), где
|
xj ≥ 0 (j = 1, 2, …, k; k ≤ n), |
3) |
при котором линейная функция F принимает оптимальное (т.е. максимальное или минимальное) значение.
Оптимальным решением (планом) задачи линейного программирования называется решение X = (x1, x2, …, xj, …, xn) системы ограничений (1), удовлетворяющее условию (3), при котором линейная функция (2) принимает оптимальное (максимальное или минимальное) значение.
Более кратко общую задачу линейного программирования можно представить в виде:
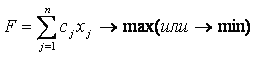
при ограничениях:
|