Задача распределения средств между предприятиями.
Для увеличения выпуска продукции, производимой n предприятиями, выделено S тыс. руб. Использование xi тыс. руб. i-м предприятием обеспечивает прирост выпуска на fi(xi). Требуется обеспечить максимальный суммарный прирост.
Необходимо исследовать эффективность вложения средств сначала в одно предприятие, затем в два и т.д. до n предприятий. Задача разбивается на n этапов.
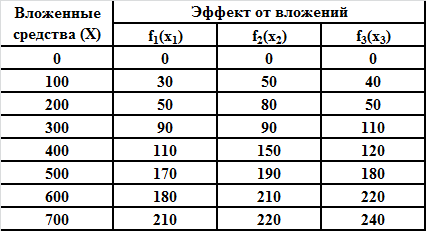
Обозначим Wi(xi) – прирост продукции на i-м предприятии при вложении xi средств. Тогда:
W1(x1) = max [f1(x1)] 0 ≤ x1 ≤ X
X – общий объем средств
W2(x2) = max [f2(x2) + W1(x - x2)] 0 ≤ x2 ≤ X
Wn(xn) = max [fn(xn) + Wn-1(x - xn)] 0 ≤ xn ≤ X
fn(xn) – прирост продукции на n-м предприятии
Wn-1 – прирост на n-1 предприятии в сумме
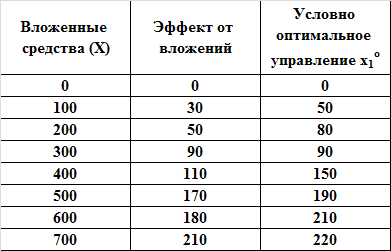
Рассмотрим одно предприятие
W1(0) = 0
W1(100) = max [f1(0) = 0; f1(100) = 30] = 30; 0 ≤ x1 ≤ 100; x1 = 100
W1(200) = max [f1(0) = 0; f1(100) = 30; f1(200) = 50] = 50; 0 ≤ x1 ≤ 200; x1=200
W1(300) = max [f1(0) = 0; f1(100) = 30; f1(200) = 50; f1(300) = 90] = 90; 0 ≤ x1 ≤ 300; x1 = 300
.....
W1(700) = max [f1(0) = 0; f1(100) = 30; f1(200) = 50; f1(300) = 90; ... f1(700) = 210] = 210; 0 ≤ x1 ≤ 700; x1 = 700
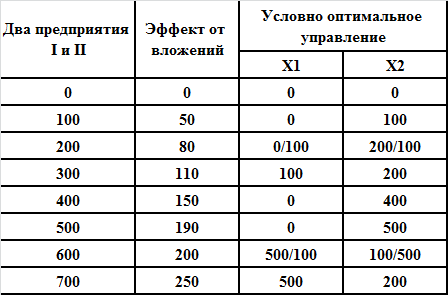
Два предприятия
W2(0) = max[f2(0) + w1(0-0)] = 0
W2(100) = max[f2(0) + w1(100-0) = 30; f2(100) + w1(100-100) = 50] = 50; 0 ≤ x2 ≤ 100 x2 = 100
W2(200) = max[f2(0) + w1(200-0) = 50; f2(100) + w1(200-100) = 80; f2(200) + w1(200-200) = 80] = 80; X2 = 200, x1 = 0 / X2 = 100 x1 = 100
W2(300) = max[f2(0) + w1(300-0) = 90; f2(100) + w1(300-100) = 100; f2(200) + w1(300-200) = 110; f2(300) + w1(300-300)=90] = 110; X2 = 200 x1 = 100
W2(400) = max[110; 140; 130; 120; 150] = 150; X2 = 400 x2 = 0
W2(500) = max[170; 180; 170; 140; 180; 190] = 190; X2 = 500 x1 = 0
W2(600) = max[180; 220; 190; 180; 200; 220; 210] = 220; X2 = 100 X1 = 500 / X2 = 500 X1 = 100
W2(700) = max[210; 230; 250; 200; 240; 240; 240; 220] = 250; X2 = 200 X1 = 500
Три предприятия
W3(700) = max[f3(700) + W2(700-700) = 240;
f3(600) + W2(700-600) = 270;
f3(500) + W2(700-500) = 260;
f3(400) + W2(700-400) = 230;
f3(300) + W2(700-300) = 260;
f3(200) + W2(700-200) = 240;
f3(100) + W2(700-100) = 260;
f3(0) + W2(700-0) = 240] = 270;
X3 = 600 x2 = 100 x1 = 0; F(x)=270
|