Пример

На АЗС имеется одна колонка. Площадка, на которой машины ожидают заправку, может вместить не более трех машин одновременно, и если она занята, то очередная машина, прибывшая к станции, в очередь не становится, а проезжает на соседнюю АЗС. В среднем машины прибывают на станцию каждые 2 мин. Процесс заправки одной машины продолжается в среднем 2,5 мин. Определить основные характеристики системы.

Решение

Математической моделью данной АЗС является одноканальная СМО с ожиданием и ограничением на длину очереди (m = 3). Предполагается, что поток машин, подъезжающих к АЗС для заправки, и поток обслуживаний – простейшие. Поскольку машины прибывают в среднем через каждые 2 мин, то интенсивность входящего потока равна λ = 1/2 = 0,5 (машин в минуту)

Среднее время обслуживания одной машины T_об = 2,5 мин, следовательно, интенсивность потока обслуживаний μ = 1/2,5 = 0,4 (машины в минуту). Определяем интенсивность нагрузки канала: α = λ/μ = 0,5/0,4 = 1,25.

Вычисляем вероятность отказа: P_отк=(α⁴(1-α))/(1-α⁵) ≈ 0,297

Относительная пропускная способность: Q = 1 - P_отк ≈ 1 - 0,297 = 0,703

Абсолютная пропускная способность: A = λQ ≈ 0,5 * 0,703 ≈ 0,352

Среднее число машин, ожидающих в очереди на заправку:

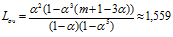
Среднее время ожидания машины в очереди находим по формуле Литтла:

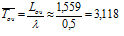
Таким образом, из анализа работы СМО следует, что из каждых 100 подъезжающих машин 30 получают отказ (P отк ≈ 29,7%), т.е. обслуживаются 2/3 заявок. Поэтому необходимо либо сократить время обслуживания одной машины (увеличить интенсивность потока обслуживаний), либо увеличить число колонок, либо увеличить площадку для ожидания.

Оптимальное решение принимается с учетом затрат, связанных соответственно с увеличением штата обслуживающего персонала (увеличение производительности канала), с расширением площадки для ожидания или приобретением дополнительной колонки, и потерь, связанных с потерей заявок на обслуживание.